Accueil > Terminale ES et L spécialité > Exercices corrigés du bac > Asie, Juin 2016 - Exercice 3 (non spé)
 Asie, Juin 2016 - Exercice 3 (non spé)
Asie, Juin 2016 - Exercice 3 (non spé)
samedi 1er avril 2017, par
Asie, Juin 2016 - Exercice 3 (non spé).
5 points - 45 minutes
Thèmes abordés : suites (géométriques), algorithmes.
Pour faire cet exercice dans de bonnes conditions, il est recommandé de connaître les méthodes suivantes :
Le 1er septembre 2015, un ensemble scolaire compte 3 000 élèves.
Une étude statistique interne a montré que chaque 1er septembre :
• 10 % de l’effectif quitte l’établissement ;
• 250 nouveaux élèves s’inscrivent.
On cherche à modéliser cette situation par une suite $(u_n)$ où, pour tout entier naturel $n$, $u_n$ représente le nombre d’élèves le 1er septembre de l’année $2015+n$.
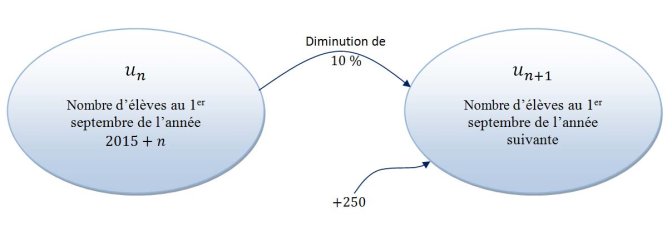
1. Justifier qu’on peut modéliser la situation avec la suite $(u_n)$ telle que $u_0=3000$ et, pour tout entier naturel $n$, $u_{n+1}=0,9u_n+250$.
Relire la méthode : Traduire un énoncé par une relation de récurrence.
2. Pour tout entier naturel $n$, on pose $v_n=u_n−2500$.
a. Démontrer que la suite $(v_n)$ est géométrique de raison 0,9. Préciser $v_0$.
Relire la méthode : Montrer qu’une suite est géométrique.
b. Exprimer, pour tout entier naturel $n$, $v_n$ en fonction de $n$.
En déduire que pour tout entier naturel $n$, $u_n=500×0,9^n+2500$.
Relire la méthode : Donner l’expression du terme général d’une suite géométrique .
3. Démontrer que pour tout entier naturel $n$, $u_{n+1}−u_n=−50×0,9^n$.
En déduire le sens de variation de la suite $(u_n)$.
Relire la méthode : Etudier les variations d’une suite par différence.
4. La capacité optimale d’accueil est de 2 800 élèves. Ainsi, au 1er septembre
2015, l’ensemble scolaire compte un sureffectif de 200 élèves.
Écrire un algorithme permettant de déterminer à partir de quelle année, le
contexte restant le même, l’ensemble scolaire ne sera plus en sureffectif.
Relire la méthode : Ecrire un algorithme de seuil.
C’est terminé !
 Mathématiques.club
Mathématiques.club