Accueil > Terminale ES et L spécialité > Suites > Traduire un énoncé par une relation de récurrence
 Traduire un énoncé par une relation de récurrence
Traduire un énoncé par une relation de récurrence
samedi 4 février 2017, par
Méthode
Etablir une relation de récurrence pour une suite $(u_n)$, c’est écrire une égalité faisant intervenir un terme quelconque et son ou ses suivant(s). Bien souvent dans les exercices de type Bac, il s’agit d’écrire une égalité faisant intervenir $u_{n+1}$ et $u_n$.
Il n’est pas toujours facile de traduire un énoncé pour établir ce type d’égalités. On peut toutefois suivre les étapes suivantes :
- Lire l’énoncé avec beaucoup d’attention et surligner les mots importants.
- Faire un schéma permettant de résumer la situation. Si l’exercice fait mention d’une suite $(u_n)$, il est nécessaire de faire apparaître (au moins) les termes $u_n$ et $u_{n+1}$ sur le schéma. Cliquer sur le schéma pour l’agrandir.
- Traduire le schéma par une égalité.
Un exemple en vidéo
D’autres exemples pour s’entraîner
- Niveau facile
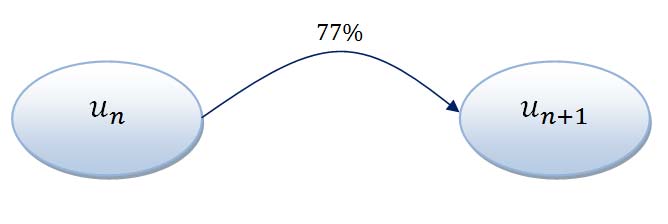
On considère une suite $(u_n)$ telle qu $u_0=8$ et chaque terme d’indice $n \ge 1$ vaut $77\%$ du précédent.
Etablir une relation de récurrence pour la suite $(u_n)$.
- Niveau facile
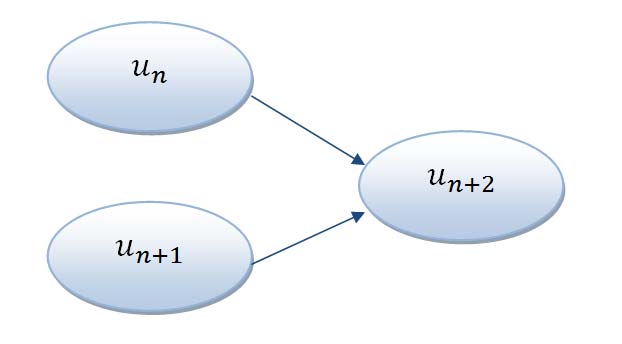
On considère une suite
- Niveau moyen
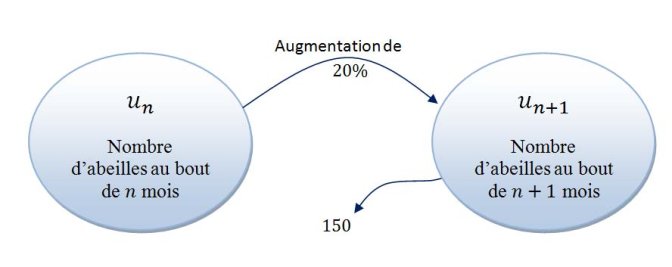
On considère une population d’abeilles dont on compte le nombre d’individus le premier jour de chaque mois. On notera
- Niveau difficile
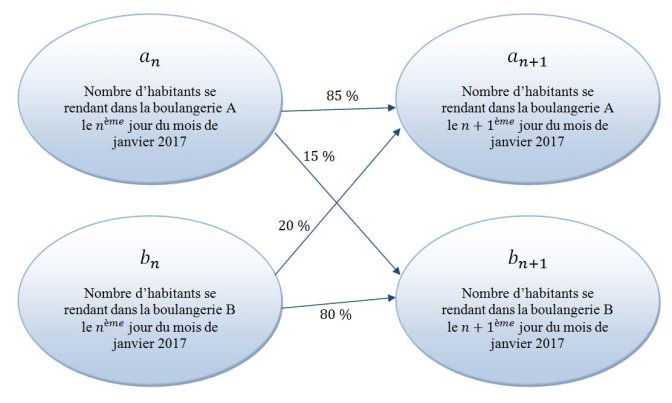
Dans un petit village, 1500 personnes vont acheter une baguette de pain tous les matins du mois de janvier 2017. Il y a deux boulangeries dans ce village. Le 1er janvier 2017, 750 habitants sont allés dans la boulangerie A et 750 dans la boulangerie B. Ensuite, d’un jour à l’autre,
– 15 % des habitants ayant acheté leur pain dans la boulangerie A vont l’acheter, le jour suivant, dans la boulangerie B. Les 85 % restants retournent dans la boulangerie A.
– 20 % des habitants ayant acheté leur pain dans la boulangerie B vont l’acheter, le jour suivant, dans la boulangerie A. Les 80 % restants retournent dans la boulangerie B.
On appelle
Au Bac
On utilise cette méthode pour résoudre :
- la question B.1 de Nouvelle Calédonie, Novembre 2016 - Exercice 2 (non spé).
- la question B.2a de Nouvelle Calédonie, Novembre 2016 - Exercice 2 (non spé).
- la question A.2 de Métropole, Septembre 2016 - Exercice 3 (non spé).
- la question 1 de Asie, Juin 2016 - Exercice 3 (non spé).
- la question 2a de Centres étrangers, Juin 2018 - Exercice 2.
 Mathématiques.club
Mathématiques.club



Messages
1. Traduire un énoncé par une relation de récurrence, 18 janvier 2019, 11:19, par bouba
merci, très clair !
2. Traduire un énoncé par une relation de récurrence, 20 janvier 2019, 17:59, par Neige
De rien, avec plaisir !